Long Answer TypeA survey regarding the heights (in cm) of 50 girls of class X of a school was conducted and the following data was obtained:
|
Height in cm |
120 - 130 |
130 - 140 |
140 - 150 |
150 - 160 |
160 - 170 |
Total |
|
Number of girls |
2 |
8 |
12 |
20 |
8 |
50 |
Find mean, median and mode of the following data:
|
Classes |
Frequency |
|
0-20 |
6 |
|
20-40 |
8 |
|
40-60 |
10 |
|
60-80 |
12 |
|
80-100 |
6 |
|
100-120 |
5 |
|
120-140 |
3 |
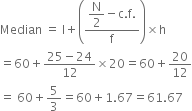
Find mean, median and mode of the following data:
|
Classes |
Frequency |
|
0 - 50 |
2 |
|
50 - 100 |
3 |
|
100 - 150 |
5 |
|
150 - 200 |
6 |
|
200 - 250 |
5 |
|
250 - 300 |
3 |
|
300 - 350 |
1 |
The following table gives the daily income of 50 workers of a factory :
|
Daily income (in Rs.) |
No. of Workers |
|
100-120 |
12 |
|
120-140 |
14 |
|
140-160 |
8 |
|
160-180 |
6 |
|
180-200 |
10 |
Find the Mean, Mode and Median of the above data.
Short Answer TypeFind the mode, median and mean for the following data :
|
Marks Obtained |
Number of Students |
|
25-35 |
7 |
|
35-45 |
31 |
|
45-55 |
33 |
|
55-65 |
17 |
|
65-75 |
11 |
|
75-85 |
1 |
Long Answer TypeThe table given below shows the frequency distribution of the scores obtained by 200 candidates in a BCA examination.
|
Score |
No. of candidates |
|
200-250 |
30 |
|
250-300 |
15 |
|
300-350 |
45 |
|
350-400 |
20 |
|
400-450 |
25 |
|
450-500 |
40 |
|
500-550 |
10 |
|
550-600 |
15 |
Draw cumulative frequency curves by using (i) 'less than series', (ii) 'more than series'.
Draw both types of cumulative freqneucy curve on the same graph paper and then determine the median.
|
Marks obtained |
No. of students |
|
50-60 |
4 |
|
60-70 |
8 |
|
70-80 |
12 |
|
80-90 |
6 |
|
90-100 |
6 |
c.f. distribution table :
|
Marks |
No. of students |
c.f. (Less than) |
c.f (More tlian) |
|
50-60 |
4 |
4 |
36 |
|
60-70 |
8 |
12 |
32 |
|
70-80 |
12 |
24 |
24 |
|
80-90 |
6 |
30 |
12 |
|
90-100 |
6 |
36 |
6 |
Now, we plot the points (60,4), (70,12), (80,24), (90,30), (100,36), for less than series.
And. (50,36), (60,32), (70,24), (80,12), (90,6) for more than series.
The two curves drawn intersect each other at point, say P. Through this point P, draw a vertical line, which meets x-axis at 76.
So, median = 76
Draw 'less than' and 'more than' ogive curve from the following and indicate the value of median.
|
Marks |
No. of students (f) |
|
0-5 |
7 |
|
5-10 |
10 |
|
10-15 |
20 |
|
15-20 |
13 |
|
20-25 |
12 |
|
25-30 |
10 |
|
30-35 |
14 |
|
35-40 |
9 |
|
Daily Income (in Rs.) |
Number of Workers |
|
100-120 |
12 |
|
120-140 |
14 |
|
140-160 |
8 |
|
160-180 |
6 |
|
180-200 |
10 |
During the medical check-up of 35 students of a class their weights were recorded as follows:
|
Weight (in kg.) |
No. of Students |
|
38—40 |
3 |
|
40—42 |
2 |
|
42—44 |
4 |
|
44—46 |
5 |
|
46—48 |
14 |
|
48—50 |
4 |
|
50—52 |
3 |
Draw a less than type and a more than type ogive from the given data. Hence obtain the median weight from the graph.
Switch
