 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type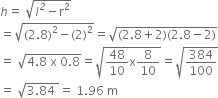
Let ‘R’ met. be the radius and ‘H’ met. be the height of the cylindrical part.
Thus,
R = 2m and H = 2.1m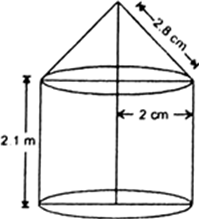
Now,
Area of the canvas used
= curved surface area of conical part + curved surface area of cylindrical part = ![]() rl + 2
rl + 2![]() RH =
RH = ![]() rl + 2
rl + 2![]() rH
rH
[∵ r = R] = ![]() r (l + 2H)
r (l + 2H)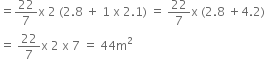
Cost of the canvas of the tent = Rs. 500 x 44 = Rs. 22,000
And.
Volume of air enclosed in the tent = Volume of the conical part + Volume of cylindrical part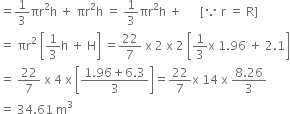
 Short Answer Type
Short Answer Type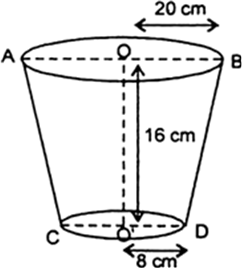
 Long Answer Type
Long Answer Type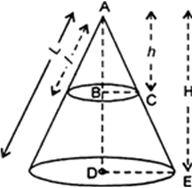
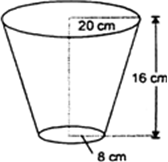
 Short Answer Type
Short Answer TypeA bucket of height 8 cm made up of copper sheets is in the form of frustum of a right circular cone with radii of its lower ends as 3 cm and 9 cm respectively. Calculate
(i) the height of the cone of which the bucket is a part.
(ii) the volume of water which can be filled in the bucket.
(iii) the area of copper sheet required to make the bucket.
