Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Three Dimensional Geometry

Short Answer Type

21.

Find the projection of the line segment joining the points (1, 2, 3), (4, 3, 1) on the line with direction ratios 3, –6, –2.

243 Views

22. Find the projection of the line segment joining the points (2, -3, 0), (0, 4, 5) on the line with direction cosines

2 over 3 comma space 3 over 7 comma space minus 6 over 7

91 Views

23.

A directed line segment makes angles 45° and 60° with x-axis and y-axis and an acute angle with z-axis. If P (– 1, 2, – 3) and Q (4, 3, 1) are two points in space, find the projection of PQ on the given line.

108 Views

Long Answer Type

24. If A and B are the points (– 1, 2, 1) and (4, 3, 5). Find the projection of AB on a line which makes angles of 120° and 135° with y-axis and z-axis respectively and acute angle with x-axis.

128 Views

25. A and B are the points (2, – 1, 3) and (4, 2, 5). Find the projection of AB on a line which is inclined at equal acute angles with the co-ordinate axes.

80 Views

26.

If P, Q, R, S are the points (– 2, 3, 4), (– 4, 4, 6), (4, 3, 5), (0, 1, 2), prove by projection that PQ is perpendicular to RS.

111 Views

27. Show that the line through the points (1, –1, 2), (3, 4, –2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).

Let P (1, –1, 2), Q (3, 4, –2), R (0, 3, 2) and S (3, 5, 6) be given points.
Direction ratios of RS are 3 - 0, 5 - 3, 6 - 2 i.e. 3, 2, 4.
∴ direction cosines of RS are
$fraction numerator 3 over denominator square root of 9 plus 4 plus 16 end root end fraction comma space space fraction numerator 2 over denominator square root of 9 plus 4 plus 16 end root end fraction comma space fraction numerator 4 over denominator square root of 9 plus 4 plus 6 end root end fraction$
i.e., $fraction numerator 3 over denominator square root of 29 end fraction comma space fraction numerator 2 over denominator square root of 29 end fraction comma space fraction numerator 4 over denominator square root of 29 end fraction$
Projection of PQ on RS
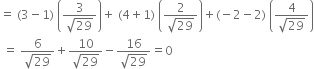
$equals space left parenthesis 3 minus 1 right parenthesis space open parentheses fraction numerator 3 over denominator square root of 29 end fraction close parentheses plus space left parenthesis 4 plus 1 right parenthesis space open parentheses fraction numerator 2 over denominator square root of 29 end fraction close parentheses plus left parenthesis negative 2 minus 2 right parenthesis space open parentheses fraction numerator 4 over denominator square root of 29 end fraction close parentheses space equals space fraction numerator 6 over denominator square root of 29 end fraction plus fraction numerator 10 over denominator square root of 29 end fraction minus fraction numerator 16 over denominator square root of 29 end fraction equals 0$