Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Three Dimensional Geometry

Long Answer Type

31. The projection of a line on the co-ordinate axes are 6, 2, 3. Find the length of the line and its direction cosines. Also, find the projection of the line segment joining (2, – 3, 1) to (4, 2, 3) on this line.

Let l, m, n be the direction cosines of the line PQ and let the length of the line segment be r.
∵ projections of the line segment on the axes are 6, 2, 3.
∴ l r = 6, m r = 2, n r = 3
Squaring and adding. we get,
(l² + m² + n²) r² = 36 + 4 + 9
∵ r² = 49 ⇒ r = 7
$therefore space space space space straight l space equals space 6 over 7 comma space straight m space equals space 2 over 7 comma space space straight n space equals 3 over 7$

∴ length of line = 7 units
and direction cosines of line PQ are

6 over 7 comma space 2 over 7 comma space 3 over 7.

We are to find projection of line segment joining A (2, -3, 1) to B (4, 2, 3) on PQ

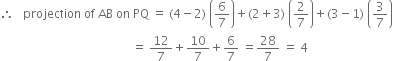
therefore space space space projection space of space AB space on space PQ space equals space left parenthesis 4 minus 2 right parenthesis space open parentheses 6 over 7 close parentheses plus left parenthesis 2 plus 3 right parenthesis space open parentheses 2 over 7 close parentheses plus left parenthesis 3 minus 1 right parenthesis space open parentheses 3 over 7 close parentheses space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space 12 over 7 plus 10 over 7 plus 6 over 7 space equals 28 over 7 space equals space 4

112 Views

32. A (– 1, 2, – 3), B (5, 0, – 6), C (0, 4, – 1) are three points. Show that the direction cosines of the bisectors of are proportional to 25, 8, 5 and -11,

AB space equals space square root of left parenthesis 5 plus 1 right parenthesis squared plus left parenthesis 0 minus 2 right parenthesis squared plus left parenthesis negative 6 plus 3 right parenthesis squared end root space space space space space space equals space square root of 36 plus 4 plus 9 end root space equals space square root of 49 space equals space 7 AC space equals space square root of left parenthesis 0 plus 1 right parenthesis squared plus left parenthesis 4 minus 2 right parenthesis squared plus left parenthesis negative 1 plus 3 right parenthesis squared end root space space space space space space space space equals space square root of 1 plus 4 plus 4 end root space equals space square root of 9 space equals space 3

88 Views

Short Answer Type

33. The cartesian equations of a line are

fraction numerator straight x minus 5 over denominator 3 end fraction space equals space fraction numerator straight y plus 4 over denominator 7 end fraction space equals fraction numerator straight z minus 6 over denominator 2 end fraction.

Find a vector equation for the line.

90 Views

34.

The Cartesian equation of a line is $fraction numerator straight x plus 3 over denominator 2 end fraction space equals space fraction numerator straight y minus 5 over denominator 4 end fraction space equals fraction numerator straight z plus 6 over denominator 2 end fraction.$ Find the vector equation for the line.

80 Views

35.

Find the cartesian equation of the line which passes through the point (-2, 4, -5) and is parallel to the line given by $fraction numerator straight x plus 3 over denominator 3 end fraction space equals space fraction numerator straight y minus 4 over denominator 5 end fraction space equals fraction numerator straight z plus 8 over denominator 6 end fraction$

109 Views

36.

Find the equations of a line which is parallel to the line $fraction numerator straight x minus 2 over denominator 3 end fraction space equals fraction numerator straight y plus 1 over denominator 1 end fraction space equals space fraction numerator straight z minus 7 over denominator 9 end fraction$ and which passes through the point (3, 0, 5).

127 Views

Long Answer Type

37.

For the cartesian and vector equation of a line which passes through the point (1, 2, 3) and is parallel to the line $fraction numerator negative straight x minus 2 over denominator 1 end fraction space equals space fraction numerator straight y plus 3 over denominator 7 end fraction space equals space fraction numerator 2 straight z minus 6 over denominator 3 end fraction.$

99 Views

Short Answer Type

38.

Find the equation of line (vector and cartesian both) which is parallel to the vector $2 straight i with hat on top space minus straight j with hat on top plus 3 space straight k with hat on top$ and which passes through the point (5, -2, 4).

76 Views

39. Find the vector equation of the line passing through the point (2, –1, –1) which is parallel to the lines 6 x – 2 = 3 y + 1 = 2 z – 2.

95 Views

40.

The equation of a line is given by $fraction numerator 4 minus straight x over denominator 2 end fraction space equals space fraction numerator straight y plus 3 over denominator 3 end fraction space equals fraction numerator straight z plus 2 over denominator 6 end fraction$ . Write the direction cosines of a line parallel to the above line.

105 Views