Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Three Dimensional Geometry

Short Answer Type

81. If the lines

fraction numerator straight x minus 1 over denominator negative 3 end fraction space equals space fraction numerator straight y minus 2 over denominator 2 straight k end fraction space equals space fraction numerator straight z minus 3 over denominator 2 end fraction space and space fraction numerator straight x minus 1 over denominator 3 straight k end fraction space equals space fraction numerator straight y minus 1 over denominator 1 end fraction space equals space fraction numerator straight z minus 6 over denominator negative 5 end fraction

are prependicular, then find the value of k.

88 Views

82.

Show that the lines x = ay + b, z = cy + d and x = a' y + b' , z = c' y + d' are perpendicular to each other, if aa' + cc' + 1 = 0.

331 Views

83. If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (– 4, 3, –6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.

93 Views

Long Answer Type

84. Find the equations of the line passing through the point P(–1, 3, –2) and perpendicular to the lines

straight x over 1 space equals space straight y over straight z space equals space straight z over 3 space space and space fraction numerator straight x plus 2 over denominator negative 3 end fraction space equals space fraction numerator straight y minus 1 over denominator 2 end fraction space equals space fraction numerator straight z plus 1 over denominator 5 end fraction

105 Views

85. Find the vector equation of the line passing through the point (1, 2, – 4) and perpendicular to the two lines:

fraction numerator straight x minus 8 over denominator 3 end fraction space space equals space fraction numerator straight y plus 19 over denominator negative 16 end fraction space equals space fraction numerator straight z minus 10 over denominator 7 end fraction space and space fraction numerator straight x minus 15 over denominator 3 end fraction space equals space fraction numerator straight y minus 29 over denominator 8 end fraction space equals space fraction numerator straight z minus 5 over denominator negative 5 end fraction.

92 Views

86. Show that, if the axes are rectangular, then the equations of the line through (α, β, γ) right angles to the lines

straight x over straight l subscript 1 space equals space straight y over straight m subscript 1 space equals space straight z over straight n subscript 1 comma space space straight x over straight l subscript 2 space equals space straight y over straight m subscript 2 space equals space straight z over straight n subscript 2

are

fraction numerator straight x minus straight alpha over denominator straight m subscript 1 space straight n subscript 2 minus straight m subscript 2 straight n subscript 1 end fraction space equals space fraction numerator straight y minus straight beta over denominator straight n subscript 1 straight l subscript 2 minus straight n subscript 2 straight l subscript 1 end fraction space equals fraction numerator straight z minus straight gamma over denominator straight l subscript 1 straight m subscript 2 minus straight l subscript 2 straight m subscript 1 end fraction.

82 Views

87. If the straight lines having direction cosines given by al + bm + cn = 0 and fmn + gnI + hIm = 0 are perpendicular, then show that

straight f over straight a plus straight g over straight b plus straight h over straight c space equals space 0

130 Views

Short Answer Type

88. Find the coordinates of the foot of perpendicular drawn from the point A (1, 2, 1) to the line joining B (1, 4, 6) and (5, 4, 4). Also find the perpendicular distance of A from line BC.

The equation of line through B (1, 4, 6) and C (5, 4, 4) is

fraction numerator straight x minus 1 over denominator 5 minus 1 end fraction space equals fraction numerator straight y minus 4 over denominator 4 minus 4 end fraction space equals space fraction numerator straight z minus 6 over denominator 4 minus 6 end fraction

fraction numerator straight x minus 1 over denominator 4 end fraction space equals space fraction numerator straight y minus 4 over denominator 0 end fraction space equals space fraction numerator straight z minus 6 over denominator negative 2 end fraction space equals space straight k

Any point D on it is (4 k+1 , 4, –2 k + 6)
Let D be foot of perpendicular from A on BC.

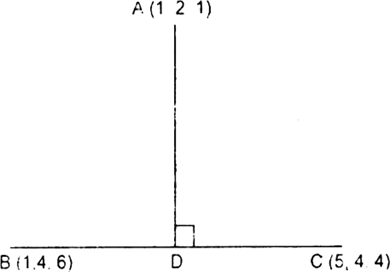
Direction ratios of AD are 4 k + 1 – 1, 4 – 2, – 2 k + 6 – 1
i.e.. 4 k , 2, – 2 k + 5
Direction ratios of BC are 4, 0, – 2
Since AD is perpendicular to BC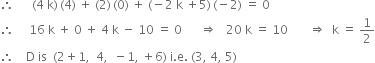
$therefore space space space space space space left parenthesis 4 space straight k right parenthesis thin space left parenthesis 4 right parenthesis space plus space left parenthesis 2 right parenthesis thin space left parenthesis 0 right parenthesis space plus space left parenthesis negative 2 space straight k space plus 5 right parenthesis thin space left parenthesis negative 2 right parenthesis space equals space 0 therefore space space space space space 16 space straight k space plus space 0 space plus space 4 space straight k space minus space 10 space equals space 0 space space space space space space rightwards double arrow space space space 20 space straight k space equals space 10 space space space space space space space rightwards double arrow space space straight k space equals space 1 half therefore space space space space straight D space is space space left parenthesis 2 plus 1 comma space space 4 comma space space minus 1 comma space plus 6 right parenthesis space straight i. straight e. space left parenthesis 3 comma space 4 comma space 5 right parenthesis$
⊥ distance of A from BC = distance AD
$equals space square root of left parenthesis 3 minus 1 right parenthesis squared plus left parenthesis 4 minus 2 right parenthesis squared plus left parenthesis 5 minus 1 right parenthesis squared end root space equals space square root of 4 plus 4 plus 16 end root space equals square root of 24 space equals space 2 square root of 6$

89 Views

89. Find the co-ordinates of the foot of the perpendicular drawn from the point A(1, 8, 4) to the line joining the points B (0, –1, 3) and C (2, – 3, – 1).

86 Views

Long Answer Type

90. Find the foot of perpendicular from the point (0, 2, 3) on the line

fraction numerator straight x plus 3 over denominator 5 end fraction space equals fraction numerator straight y minus 1 over denominator 2 end fraction space equals space fraction numerator straight z plus 4 over denominator 3 end fraction

90 Views