Take O, a comer of the rectangular parallelopipied, as origin and OA, OB, OC, the three edges through it as the axes.

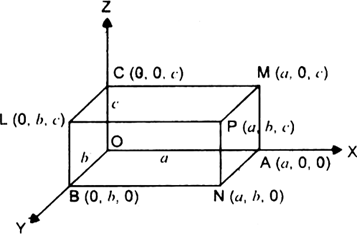
Let ΔA = a, OB = b, OC = c, then the co-ordinates of O, A, B, C are (0, 0, 0), (a, 0, 0), (0, b, 0), (0, 0, c) respectively.
The co-ordinates of other points are shown in the figure.
The four diagonals are OP, AL, BM, CN
Direction-cosines of OP are a – 0, b – 0, c – 0 i.e., a, b. c respectively
Direction-cosines of AL are 0 – a, b – 0, c – 0 i.e., – a, b. c respectively
Direction-cosines of BM are a – 0, 0 – b, c – 0 i.e., a,– b, c respectively
Direction-cosines of CN are a – 0, b – 0, 0 – c i.e., a, b, – c respectively.
Let θ be the angle between OP and AL.


 angle between OP and AL = 
Similarly angle between OP and BM = 
and angle between OP and CN = 
Proceeding in this way, we see that angles between four diagonals are given by