Short Answer Type
Long Answer Type
Since < l, m, n > and < l + δl, m + δm, n + δn > are direction cosines of two lines
∴ l2 + m2 + n2 = 1 ...(1)
and (l + δl)2 + (m + δm)2 + (n2 + δn)2 = 1
or (l2 + m2 + n2) + 2 (l δl + m δm + n δn) + [(δl)2 + (δm)2 + (δn)2] = 1
or 1+2 (I δl + m δm + n δn) + [ (δl)2 + (δm)2 + (δn)2 ] = 1 [∵ of (1)]
or (δl)2 + (δm)2 + (δn)2 = – 2 (lδ l + m δm) + n δn) ....(2)
Now δθ is angle between two lines
∴ cos δθ = l (l + δl) + m (m + δm) + n (n + δn)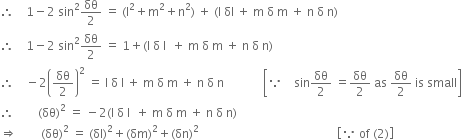
Find the angle between the two lines whose direction cosines are given by the equations:
l + m + n = 0, l2 + m2 – n2 = 0
Switch
