 Short Answer Type
Short Answer TypeIn each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
2x + 3 y – z = 5
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
5y + 8 = 0
 Long Answer Type
Long Answer TypeIn the following cases, find the coordinates of the foot of the perpendicular
drawn from the origin.
2x + 3y + 4z – 12 = 0
 Short Answer Type
Short Answer Type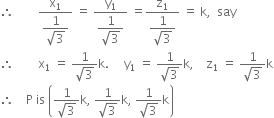
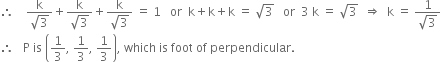
 Long Answer Type
Long Answer Type