The equations of given planes are
7x + 5y + 6z + 30 = 0    ...(1)
and 3x – y – 10z + 4 = 0    ...(2)
Direction ratios of normal to plane (1) are 7, 5, 6
Direction ratios of normal to plane (2) are 3, –1, –10.
Now 
∴    planes (1) and (2) are not parallel.
Again (7) (3) + (5) (– 1) + (6) (– 10) = 21 – 5 – 60 = – 44 ≠ 0
∴  planes (1) and (2) are not perpendicular to each other.
Let θ be angle between planes (1) and (2).
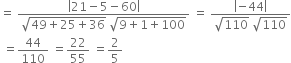