The equations of given planes are
                       
and                 

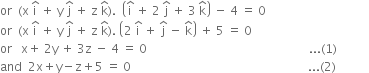
Any plane through the intersection of planes (1) and (2) is
(x + 2 y + 3 z – 4) + k (2 x + y – z + 5) = 0    ...(3)
i.e. (2 k + 1) x + (k + 2) y + (– k + 3) z + (5 k – 4) = 0
Direction ratios of the its normal are 2 k + 1, k + 2, – k + 3.
Again consider the plane
                        
or              
or                                                        ...(4)

Direction ratios of its normal are 5, 3, -6
Since plane (3) is perpendicular to plane (4)
∴ 5 (2 k + 1) + 3 (k + 2) + (–6) (– k + 3) = 0
∴ 10 k + 5 + 3 k + 6 + 6 k – 18 = 0

Putting 
                
or 19 (x + 2y + 3z – 4) + 7 (2 x + y – z + 5) = 0
or 19x+ 38y + 57z – 76 + 14x + 7y – 7z + 35 = 0
or 33x + 45y + 50z – 41 = 0
which is required equation of plane.