 Long Answer Type
Long Answer TypeIn the Fig., ABC is a triangle in which AB = AC points D and E are points on the sides AB and AC respectively such that AD = AE. Show that the points B, C, E and D are concyclic.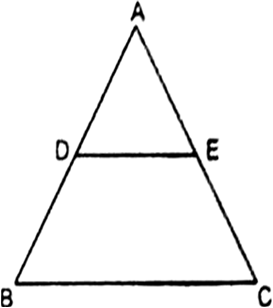

In an equilateral triangle ABC, AD is the altitude drawn from A on side BC. Prove that:
3AB2 = 4AD2.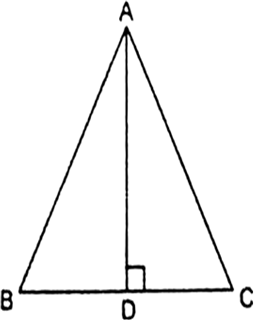
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type