 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type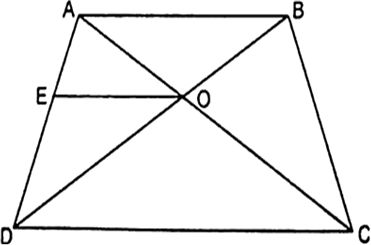
 Short Answer Type
Short Answer TypeIn the given fig. ∆ODC ~ ∆OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.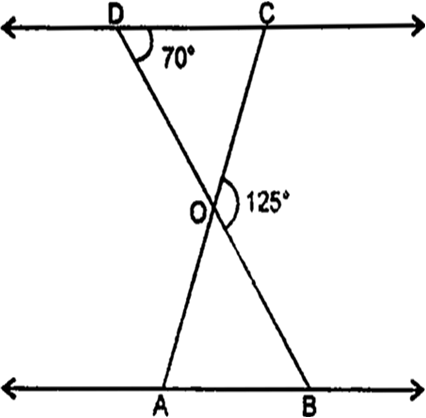
∠DOC + ∠BOC = 180° [Linear pair]
⇒ ∠DOC + 125° = 180
⇒ ∠DOC = 180 - 125
⇒ ∠DOC = 55°
In ∆DOC, we have
∠DOC + ∠ODC + ∠DCO = 180°
[Angle sum property of triangle]
⇒ 55° + 70° + ∠DCO = 180°
⇒ 125° + ∠DCO = 180°
⇒ ∠DCO =180° - 125°
⇒ ∠DCO = 55°
∵ ∆ODC ~ ∆OBA [Given]
∴ ∠OCD = ∠OAB
⇒ ∠DCO = ∠OAB
⇒ ∠OAB = ∠DCO
But ∠DCO = 55°
⇒ ∠OAB = 55°.
