Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeIn the given Fig, altitudes AD and CE of ![]() intersects each other at the point P. Show that:
intersects each other at the point P. Show that:
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC.

AD and CE are altitudes, which intersect each other at P.
(i) In ∆AEP and ∆CDP
∠AEP = ∠CDP = 90° [given]
and ∠APE = ∠CPD
[vertically opposite angles]
Therefore, by using AA similar condition
∆AEP ~ ∆CDP.
(ii) In ∆ABD and ∆CBE
∠ADB = ∠CEB = 90° [given]
and ∠B = ∠B [common]
Therefore, by using AA similar condition
∆ABD ~ ∆CBE.
(iii) In ∆AEP and ∆ADB
∠AEP = ∠ADB = 90° [given]
and ∠PAE = ∠DAB [common]
Therefore, by using AA similar condition
∆AEP ~ ∆ADB
(iv) In ∆PDC and ∆BEC
∠PDC = ∠CEB = 90° [given]
∠PCD = ∠ECB [common]
Therefore, by using AA similar condition
∆PDC ~ ∆BEC.
 Short Answer Type
Short Answer TypeIn the given fig, ABC and AMP are two right triangles, right angled at B and M respectively.
Prove that:
(i) ![]()
(ii) ![]()

 Long Answer Type
Long Answer TypeCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC ~ ΔFEG, show that:
(i) ![]()
(ii) ![]()
(iii) ![]()
 Short Answer Type
Short Answer TypeIn the given fig, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC. Prove that ∆ABD ~ ∆ECF.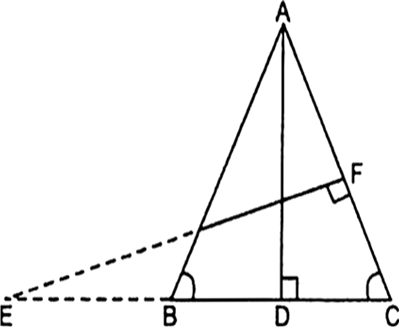
 Long Answer Type
Long Answer Type