 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer TypeA ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
 Long Answer Type
Long Answer TypeTwo poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
 Short Answer Type
Short Answer Type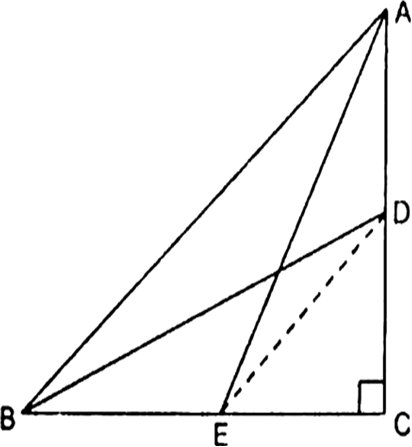
Given : A right triangle ABC, right angled at C. D and E are points on sides AC and BC respectively.
To Prove : AE2 + BD2 = AB2 + DE2
Const: Join AE, BD and DE.
Proof: In ∆ACE
AE2 = AC2 + CE2 ...(i)
[Using Pythagoras theorem]
In ∆BCD, BD2 = CD2 + BC2 ...(ii)
[Using Pythagoras theorem]
Adding (i) and (ii), we get
AE2 + BD2 = (AC2 + BC2) + (CE2 + CD2)
⇒ AE2 + BD2 = AB2 + DE2 Hence Proved.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type