 Long Answer Type
Long Answer TypeIn the given fig., D is a point on hypotenuse AC of┬ĀŌłåABC, DIM ŌŖź BC and DN ŌŖź AB.┬Ā
Prove that:
(i) DM2┬Ā= DN ├Ś MC.
(ii) DN2┬Ā= DM ├Ś AN.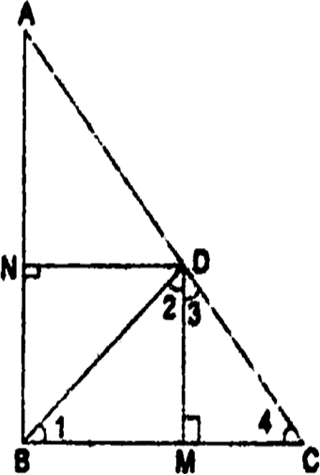
 Short Answer Type
Short Answer TypeIn the given fig., ABC is a triangle┬Āin which ŌłĀABC > 90┬░ and AD ŌŖź CB produced. Prove that AC2┬Ā= AB2┬Ā+ BC2┬Ā+ 2 BC . BD.
In the given Fig,┬Ā┬ĀABC is a triangle in which ŌłĀABC < 90┬░ and AD ŌŖź BC. Prove that AC2= AB2┬Ā+ BC2┬Ā- 2 BC.BD.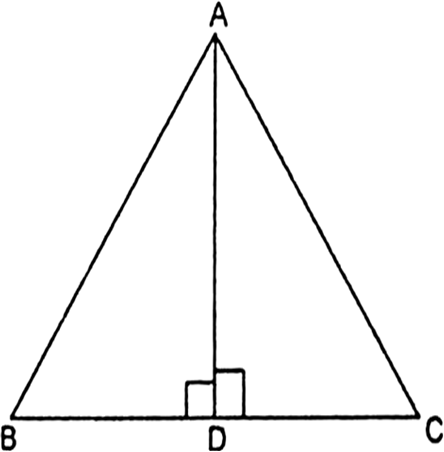
 Long Answer Type
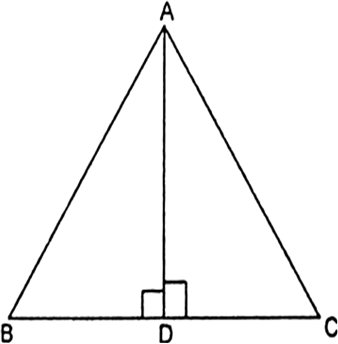
Long Answer TypeIn the given fig, AD is a median of┬Āa triangle ABC and AM ŌŖź BC. Prove that:
(i) ┬Ā ┬Ā![]()
(ii)┬Ā![]()
(iii) ┬Ā┬Ā![]()
In the given fig,┬Ātwo chords AB and CD intersect each other at the point P. Prove that:
(i) ŌłåAPC ~ ŌłåDPB.
(ii) AP . PB = CP . DP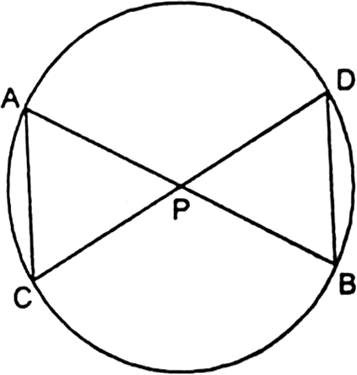
In the given Fig,┬Ātwo chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ŌłåPAC ~ ŌłåPDB.
(ii) PA. PB = PC . PD.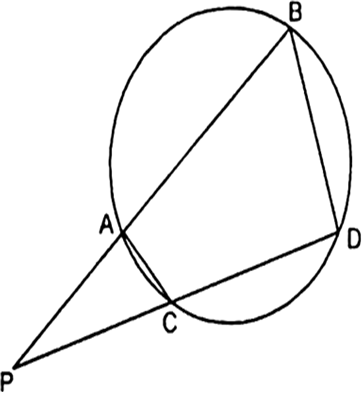
In the given fig, D is a point on side BC of┬ĀŌłåABC such that ┬Ā![]() ┬ĀProve that AD is the bisector of┬ĀŌłĀBAC.
┬ĀProve that AD is the bisector of┬ĀŌłĀBAC.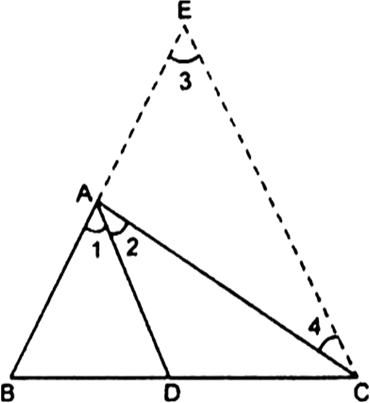
ŌłĄ ┬Ā┬Ā┬ĀAC = AE [By construction]
Ōł┤ ┬Ā┬Ā┬ĀŌłĀ3 = ŌłĀ4 ┬Ā┬Ā┬Ā...(iii)[Angles opposite equal sides of a triangle are equal]
Using (iii), (i) and (ii), we getŌłĀBAD = ŌłĀCAD
Hence, AD is the bisector of ŌłĀBAC.