Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

241. In Fig. DE || BC and

space AD over DB equals 3 over 5.

If AC = 4.8 cm, find the length of AE.

652 Views

242. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE ~ ∆CFB.

862 Views

243.

In the given fig., $PS over SQ equals PT over TR$ and ∠PST = ∠PRQ. Prove that ∆PQR is an isosceles triangle.

219 Views

244.

In the given fig, ∆ABD is a right triangle, right angled at A and AC ⊥ BD. Prove that AB² = BC. BD.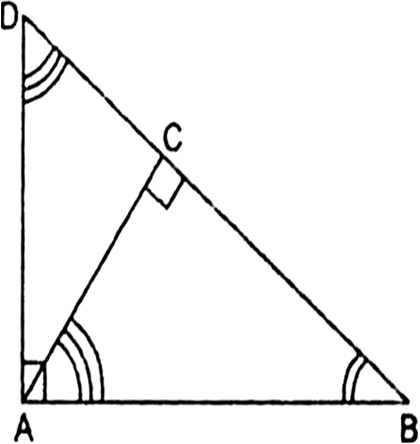

201 Views

245.

In the given fig, AB || DC. Find the value of x.

1047 Views

246.
In the given fig, express x in terms of a, b and c.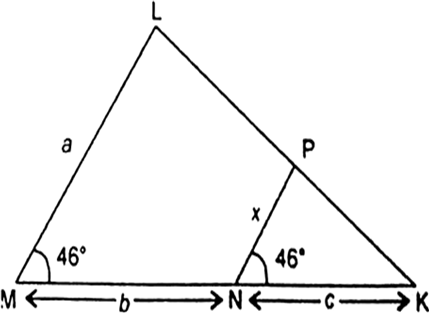

In ∆KPN and ∆KLM, we have
∠KNP = ∠KML = 46° [Given]
∠K = ∠K [Common]
∴ $increment KNP space tilde space space increment KML$
[Using AA similar condition]
$rightwards double arrow$ $space space KN over KM equals NP over ML$
[∵ Corresponding sides of similar triangles are proportional]
$space rightwards double arrow space space space space space space space space space space space space fraction numerator straight c over denominator straight b plus straight c end fraction equals straight x over straight a space space space rightwards double arrow space space space straight x space equals space fraction numerator ac over denominator straight b plus straight c end fraction.$

2955 Views

247.

In the given fig, $OA over OC equals OD over OB.$ Prove that ∠A = ∠C and ∠B = ∠D.

82 Views

Long Answer Type

248. The diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Prove that DF × EF = FB × FA.

1489 Views