 Short Answer Type
Short Answer TypeIn the given fig.,┬Ā![]() ┬Āand┬ĀŌłĀPST = ŌłĀPRQ. Prove that ŌłåPQR is an isosceles triangle.
┬Āand┬ĀŌłĀPST = ŌłĀPRQ. Prove that ŌłåPQR is an isosceles triangle.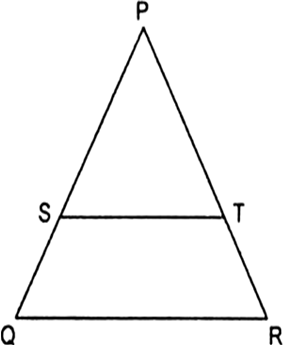
In the given fig,┬ĀŌłåABD is a right triangle, right angled at A and AC ŌŖź BD. Prove that┬ĀAB2┬Ā= BC. BD.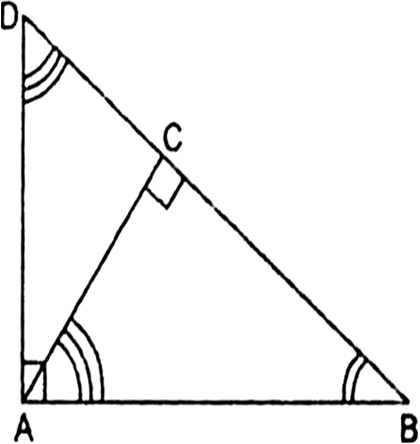
┬Ā
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeIn ŌłåABD and ŌłåAEC, we have
ŌłĀADB = ŌłĀAEC
[Each equal to 90┬░]
ŌłĀBAD = ŌłĀEAC [Common]![In ŌłåABD and ŌłåAEC, we haveŌłĀADB = ŌłĀAEC[Each equal to 90┬░]ŌłĀBA](/application/zrc/images/qvar/MAEN10042228.png)
So, by AA-criterion of similarity, we have
ŌłåBDA ~ ŌłåCEA or ŌłåADB ~ ŌłåAEC
Clearly, ŌłåCDB is not similar to ŌłåBEC, because they are not equiangular.
