 Long Answer Type
Long Answer TypeIn the given Fig, two triangles ABC and DBC lie on the same side of base BC. P is a point on BC such that PQ || BA and PR || BD. Prove that: QR || AD.   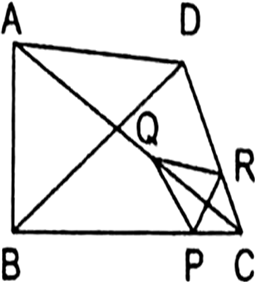
 Short Answer Type
Short Answer TypeIn the given fig,¬†ST || QR, PS = 2 cm and SQ = 3 cm. What is the ratio of the area of вИЖPQR to the area of вИЖPST?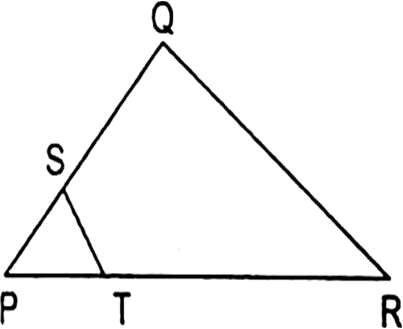
In the given Fig.¬†PB and QA are perpendiculars to segment AB. If PO = 5 cm, QO = 7 cm and area¬†вИЖPOB = 150 cm2¬†find the area of вИЖQOA.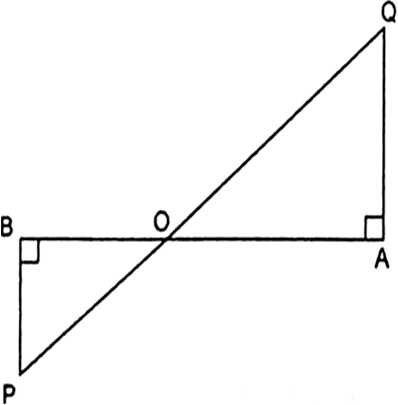
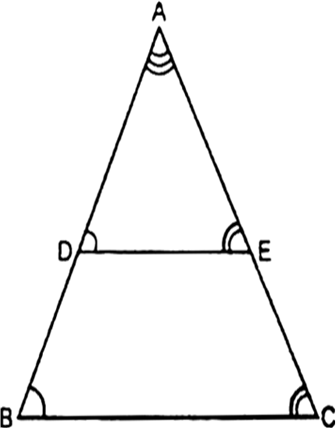
In вИЖADE,
DE || BC (Given)
вИі вИ†D = вИ†B, вИ†E = вИ†C ¬†¬†¬†[corres. вИ†s]
and ¬†¬†¬†вИ†A = вИ†A ¬†¬†¬†[Common]
вИі вИЖADE ~ вИЖABC
[A.A.A. Similarity]![]()        
       ![]()
![]()          
         ![]()
![]()      
     ![]()
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeIn the given fig, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of¬†вИЖABC to the area of вИЖADE?
