Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeIn the given Fig. DEFG is a square and ∠BAC = 90°. Prove that
(i) ∆AGF ~ ∆DBG.
(ii) ∆AGF ~ ∆EFC.
(iii) ∆DBG ~ ∆AEFC
(iv) DE2 = BD × EC.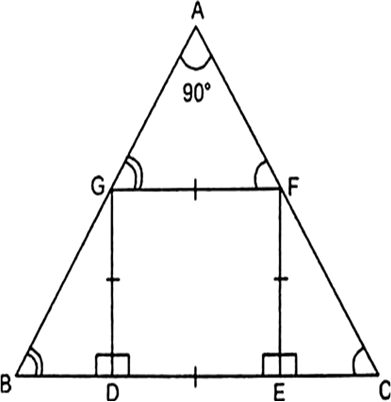
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type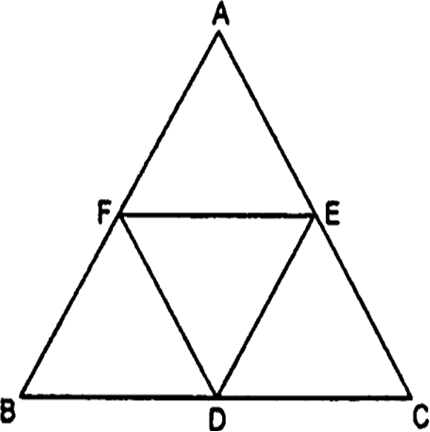
To Prove: Each of the triangles AFE, FBD, EDC and DEF are similar to ∆ABC.
Proof: F and E are the mid points of sides AB and AC respectively.
Therefore, FE || BC
[Using mid-point theorem]
Now, in ∆AFE and ∆ABC
∠AFE = ∠B [Corresponding angles]
and ∠A = ∠A [Common]
Therefore, by using AA similar condition
∆AFE ~ ∆ABC
Similarly, ∆FBD ~ ∆ABC
and ∆EDC ~ ∆ABC
∴ DE || AB
⇒ DE || AF ...(i)
and DF || AC
⇒ DF || AE ...(ii)
Comparing (i) and (ii), AEDF is a parallelogram, Similarly BDEF is a parallelogram
Now, in ∆ABC and ∆DEF
∠A = ∠EDF
and ∠B = ∠DEF
[opposite angles of parallelogram]
Therefore, by using AA similar condition
∆ABC ~ ∆DEF
Thus, each of the triangles AFE, FBD, EDC and DEF arc similar to a ∆ABC.
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type