 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeIn the given Fig.¬†DEFG is a square and ‚ą†BAC = 90¬į. Prove that
(i) ‚ąÜAGF ~ ‚ąÜDBG.
(ii) ‚ąÜAGF ~ ‚ąÜEFC.
(iii) ‚ąÜDBG ~ ‚ąÜAEFC
(iv) DE2 = BD × EC.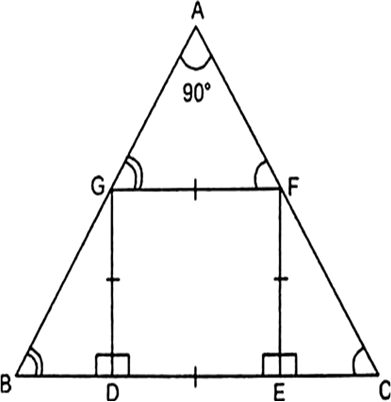
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type
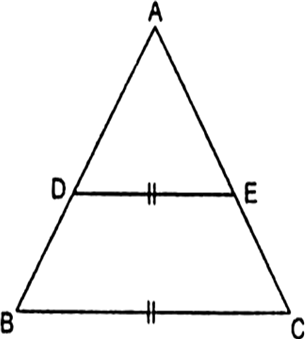
In ‚ąÜADE and ‚ąÜABC
‚ą†ADE = ‚ą†ABC
[corresponding angles]
and ¬†¬†¬†‚ą†A = ‚ą†A ¬†¬†¬†[common]
Therefore, by using AA similar condition
                ![]()
![]()            
           ![]()
![]()                 
                ![]()           ...(i)
          ...(i)
[taking reciprocals of both sides]
It is given that,![]()               
              ![]()
![]()            
           ![]()
![]()           
          ![]()
                                   [Adding '1' both side]![]()              
             ![]()
![]()               
              ![]()                     ...(ii)
                    ...(ii)
Comparing (i) and (ii), we get![]()
