 Long Answer Type
Long Answer Type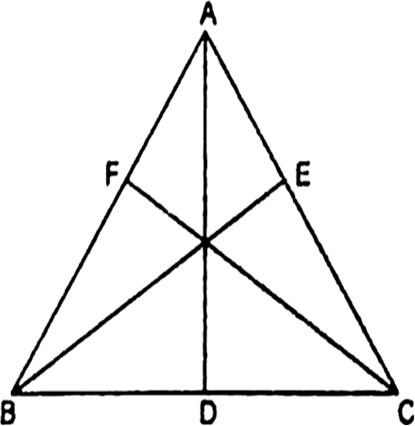
Given: A ∆ABC in which medians drawn to the sides BC, CA and AB respectively.
To Prove : 3(AB2 + BC2 + CA2)
= 4(AD2 + BE2 + CF2)
Proof: We know that, the sum of the square of any two side is equal to twice the square of half of third side together with twice the square of median which bisects the third side.
Therefore,
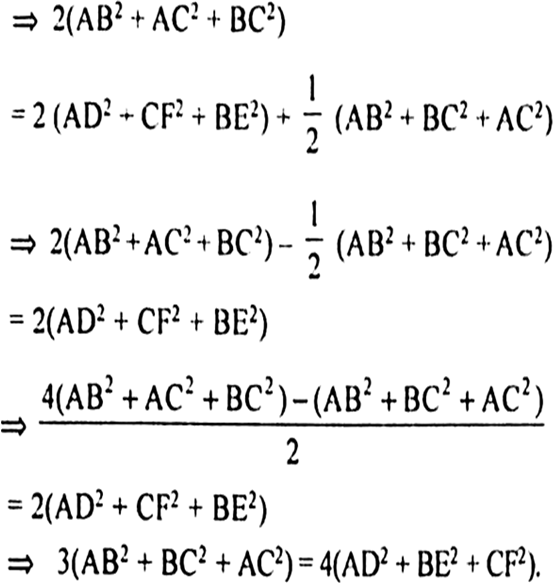
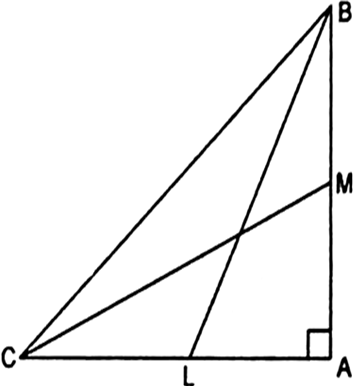
In the given Fig, ABC is a right triangle, right angled at B. AD and CE are two medians drawn from A and C respectively. If AC = 5 cm and ![]() find the length of CE.
find the length of CE.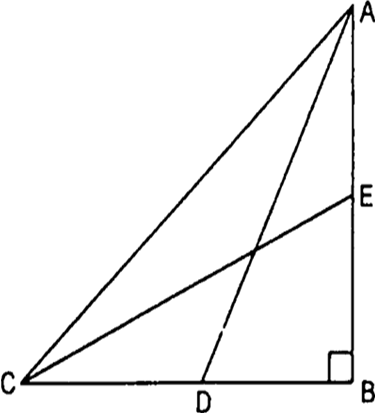
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type
