Short Answer Type
Short Answer Type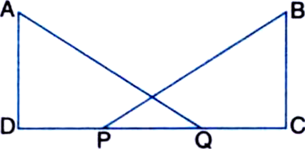
DP = CQ
‚áí DP + PQ = CQ + PQ
⇒    DQ = CP    ...(1)
In right triangles ADQ and BCP,
‚ą†ADQ = ‚ą†BCP ¬†¬†¬†[each = 90¬į]
Hyp. AQ = Hyp. BP
Side DQ = Side CP
‚ąī ‚ąÜADQ ‚ČÖ ‚ąÜBCP ¬†¬†¬†| RHS Axiom
‚ąī ‚ą†DAQ = ‚ą†CBP. ¬†¬†¬†| C.P.C.T.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type