Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

481. In figure, AD π CD and BC π CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

863 Views

482. In ∆ABC, D is the mid point of BC. The perpendiculars from D to AB and AC are equal. Prove that ∆ABC is isosceles.

207 Views

483. In figure, ∆ABD and ∆BCD are isosceles triangles on the same base BD. Prove that ∠ABC = ∠ADC.

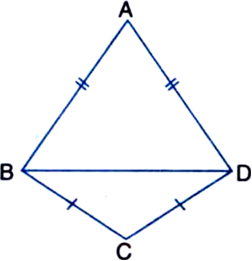
Given: ∆ABD and ∆BCD and isosceles triangles on the same base BD.
To Prove: ∠ABC = ∠ADC
Proof: ∵ ∆ABD is isosceles
∴ AB = AD
∴ ∠ABD = ∠ADB ...(1)
| Angles opposite to equal sides of a triangle are equal
∵ ∆CBD is isosceles
∴ CB = CD
∴ ∠CBD = ∠CDB ...(2)
| Angles opposite to equal sides of a triangle are equal
Adding (1) and (2), we get,
∠ABD + ∠CBD = ∠ADB + ∠CDB
⇒ ∠ABC = ∠ADC

745 Views

Long Answer Type

484. In ∆’s ABC and PQR, AB = PQ, AC = PR and altitude AM and altitude PN are equal. Show that ∆ABC ≅ ∆PQR.

1256 Views

485. In figure, the perpendicular AD, BE and CF drawn from the vertices A, B and C respectively of ∆ABC are equal. Prove that the triangle is an equilateral triangle.

1480 Views

486. ABCD is a parallelogram. If the two diagonals are equal, find the measure of ∠ABC.

309 Views

Short Answer Type

487. AB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see figure). Show that the line PQ is the perpendicular bisector of AB.

691 Views

488. P is a point equidistant from two lines l and m intersecting at point A (see figure). Show that the line AP bisects the angle between them.

615 Views

489.

In the figure, RS = QT and QS = RT. Prove that PQ = PR.

627 Views

490. In the given figure, D is the mid-point of base BC, DE and DF are perpendiculars to AB and AC respectively such that DE = DF. Prove that ∠B = ∠C.

102 Views