Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

491. ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.

408 Views

492. Show that in a right angled triangle, the hypotenuse is the longest side.

Let ABC be a right angled triangle in which ∠B = 90°.
Then, ∠A + ∠C = 90°
| ∵ Sum of all the angles of a triangle is 180°
∴ ∠B = ∠A + ∠C
∴ ∠B > ∠A
and ∠B > ∠C
∴ AC > BC
| ∵ Side opposite to greater angle is longer
and AC > AB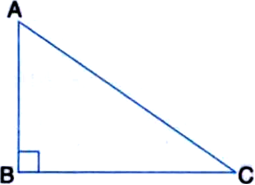

∴ AC is the longest side, i.e., hypotenuse is the longest side.

211 Views

493. In figure, sides AB and AC of ∆ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

420 Views

494. In figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

123 Views

495. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠A > ∠C and ∠B > ∠D.

495 Views

496. In figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

419 Views

497. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

274 Views

498. Prove that the sum of three altitudes of a triangle is less than the sum of the three sides of the triangle.

3380 Views

499. In figure, AD is a median of ∆ABC. Prove that AB + AC > 2AD.

[Hint. Produce AD to E such that AD = DE and join C and E.]

Prove that the sum of any two sides of a triangle is greater than twice the length of median drawn to the third side.

687 Views

500.

Prove that the sum of the three sides of a triangle is greater than the sum of its three medians.

Prove that the perimeter of a triangle is greater than the sum of its three medians.

1812 Views