 Short Answer Type
Short Answer Type
[Hint. Produce AD to E such that AD = DE and join C and E.]
OR
Prove that the sum of any two sides of a triangle is greater than twice the length of median drawn to the third side. 
Construction: Produce AD to E such that AD = DE and join C and E.
Proof.: In ‚ąÜADB and ‚ąÜEDC,
AD = DE    | By const.
BD = DC
| ‚ąĶ AD is a median of ‚ąÜABC ‚ą†ADB = ‚ą†EDC
| Vertically Opposite Angles
‚ąī ‚ąÜADB ‚ČÖ ‚ąÜEDC ¬†¬†¬†| SAS Axiom
‚ąī AB = EC ¬†¬†¬†...(1) | C.P.C.T.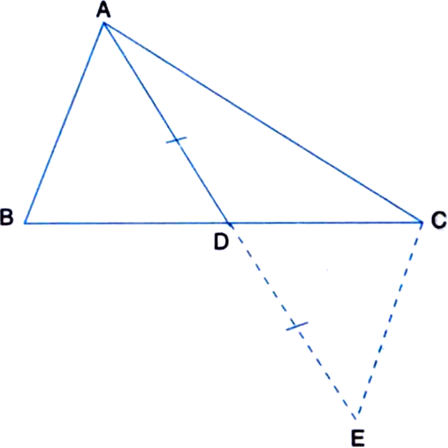
In ‚ąÜAEC,
AC + EC >  AE
‚ąĶ The sum of any two sides of a triangle is greater than the third side
⇒ AC + AB >  AE    | From (1)
⇒ AB + AC >  AE
⇒ AB + AC >  2AD.    | By const.
Prove that the sum of the three sides of a triangle is greater than the sum of its three medians.
OR
Prove that the perimeter of a triangle is greater than the sum of its three medians.
