Short Answer Type
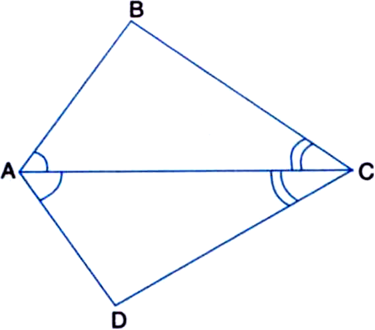
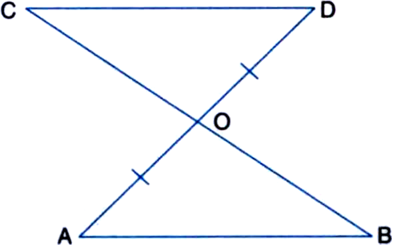
AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.
Given: ∠QPR = ∠PQR and M and N are respectively points on side QR and PR of ∆PQR, such that QM = PN.
To Prove: OP = OQ, where O is the point of intersection of PM and QN.
Proof: In ∆PNQ and ∆QMP,
PN = QM | Given
PQ = QP | Common
∠QPN = ∠PQM | Given
∴ ∆PNQ ≅ ∆QMP
| SAS congruence rule
∴ ∠PNQ = ∠QMP | CPCT
Again, in ∆PNO and ∆QMO,
PN = QM | Given
∠PON = ∠QOM
| Vertically opposite angles
∠PNO = ∠QMO | Proved above
∴ ∆PNO ≅ ∆QMO
| AAS congruence rule
∴ OP = OQ | CPCT
Long Answer TypeShort Answer Type
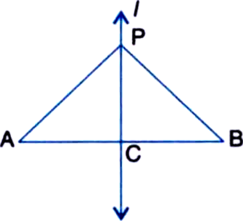
Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that: (i) ∆AOB ≅ ∆DOC (ii) O is also the mid-point of BC.
Switch
