Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

11. In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

3784 Views

12.

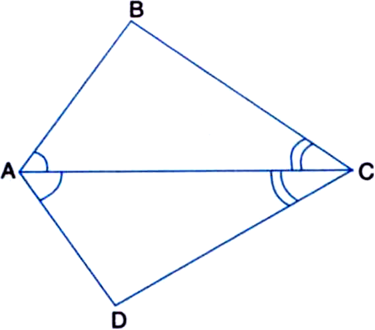
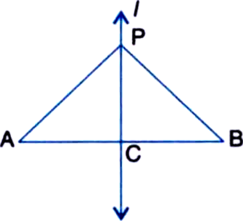
AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

883 Views

13. In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

1215 Views

Long Answer Type

14. Prove that the medians of an equilateral triangle are equal.

Given: ABC is an equilateral triangle whose medians are AD, BE and CF.
To Prove: AD = BE = CF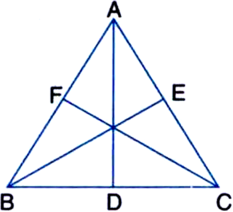

Proof: In ∆ADC and ∆BEC,

AC = BC

   $left enclose table row cell space because increment ABC space is space equilateral end cell row cell therefore space AB equals BC equals CA end cell end table end enclose$

   $angle ACD equals angle BCE$

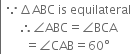
$left enclose table row cell because increment ABC space is space equilateral end cell row cell therefore angle ABC equals angle BCA end cell row cell equals angle CAB equals 60 degree end cell end table end enclose space space space space$

DE = EC

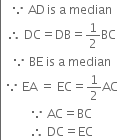
   $left enclose table row cell because space AD thin space is space straight a space median end cell row cell therefore space DC equals DB equals 1 half BC end cell row cell because space BE space is space straight a space median end cell row cell because space EA space equals space EC equals 1 half AC end cell row cell because space AC equals BC end cell row cell therefore space DC equals EC end cell end table end enclose$

$therefore space space space space increment ADC equals increment BEC space space space space space space space space space space space space space space space space space space space space space space space space$
| SAS congruence rule

$therefore$ $increment AD equals BE$ ....(1) | CPCT

Similarly, we can prove that
BE = CF ...(2)
and CF = AD ...(3)
From (1), (2) and (3)
AD = BE = CF

4736 Views

Short Answer Type

15. In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

1248 Views

16.

In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.

245 Views

17. In the given figure, if AB = FE, BC = ED, AB ⊥ BD and FE ⊥ EC, then prove that AD = FC.

514 Views

18.

In figure, OA = OB and OD = OC. Show that:
(i) ∆AOD ≅ ∆BOC and (ii) AD = BC.

395 Views

19. AB is a line segment and line l is its perpendicular bisector. If a point P lies on I, show that P is equidistant from A and B.

1973 Views

20.

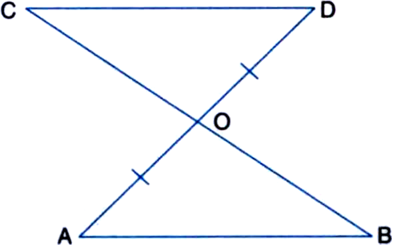
Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that: (i) ∆AOB ≅ ∆DOC (ii) O is also the mid-point of BC.

728 Views