Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

21. In the figure, ∠BCD = ∠ADC and ∠ACB = ∠BDA. Prove that AD = BC and ∠A = ∠B.

807 Views

22. In figure, AX = BY and AX || BY. Prove that ∆APX ≅ ∆BPY.

250 Views

23. In figure, if ∠AEO = ∠CDO and AB = CB, prove that ∆ABD ≅ ∆CBE.

344 Views

24. In figure, if ∠ABD = ∠ACE and AB = AC. Prove that ∆ABD ≅ ∆ACE.

1312 Views

25. In the figure given below, ABCD is a quadrilateral in which diagonal AC bisects ∠A and ∠C, prove that ∆ABC ≅ ∆ADC.

243 Views

26. In the figure below, the diagonal AC of quadrilateral ABCD bisects ∠BAD and ∠BCD. Prove that BC = CD.

848 Views

27. In the following figure, AD is the bisector of ∠A of ∆ABC. PQ and PR are perpendiculars from any point lying on AD, P to sides AB and AC respectively. Show that ∆PQA ≅ ∆PRA and PQ = PR.

283 Views

28.

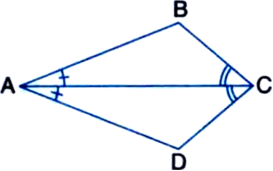
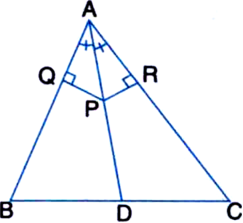
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:

(i) OB = OC
(ii) AO bisects ∠A.

1230 Views

29. In ∆ ABC, AD is the perpendicular bisector of BC (see figure). Show that A ABC is an isosceles triangle in which AB = AC.

778 Views

30. ABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (see figure). Show that these altitudes are equal.

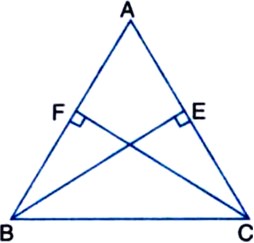
Given: ABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively.
To Prove: BE = CF.
Proof: ∵ ABC is an isosceles triangle
∴ AB = AC
∴ ∠ABC = ∠ACB    ...(1)
| Angles opposite to equal sides of a triangle are equal
In ∆BEC and ∆CFB,
∠BEC = ∠CFB    | Each = 90°
BC = CB    | Common
∠ECB = ∠FBC    | From (1)
∴ ∆BEC ≅ ∆CFB    | By AAS Rule
∴ BE = CF.    | C.P.C.T.

588 Views