Short Answer Type
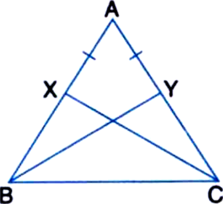
Given: A triangle ABC in which AB = AC
To Prove: ∠ABC = ∠ACB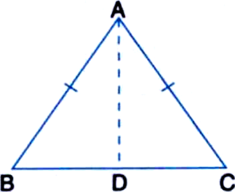
Construction: Draw the bisector AD of A so as to intersect BC at D.
Proof: In ∆ADB and ∆ADC,
AD = AD | Common
AB = AC | Given
∠BAD = ∠CAD
| By Construction
∴ ∆ADB ≅ ∆ADC
| SAS congruence rule
∴ ∠ABD = ∠ACD | CPCT
⇒ ∠ABC = ∠ACB
Yes, the converse is true.
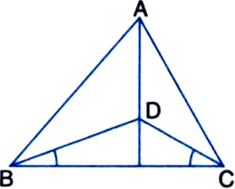
Long Answer TypeIn figure, ABCD is a square and ∠DEC is an equilateral triangle. Prove that
(i) ∆ADE ≅ ∆BCE
(ii) AE = BE
(iii) ∠DAE = 15°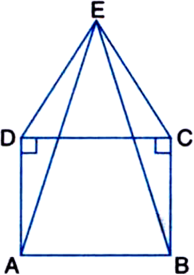
Short Answer Type
Switch
