 Short Answer Type
Short Answer Type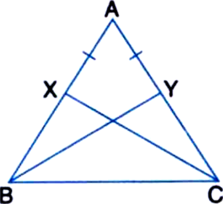
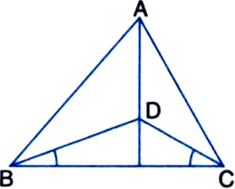
 Long Answer Type
Long Answer TypeIn figure, ABCD is a square and ∠DEC is an equilateral triangle. Prove that
(i) ∆ADE ≅ ∆BCE
(ii) AE = BE
(iii) ∠DAE = 15°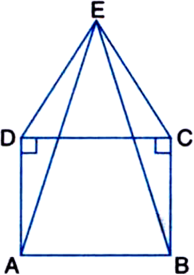
 Short Answer Type
Short Answer Type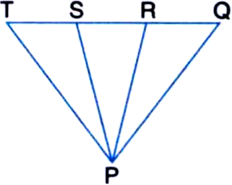
Given: PS = PR, ∠TPS = ∠QPR
To Prove: PT = PQ
Proof: In ∆PSR,
∵ PS = PR | Given
∴ ∠PSR = ∠PRS ...(1)
| Angles opposite to equal sides of a triangle are equal
⇒ ∠TPS + ∠PTS = ∠QPR + ∠PQR
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
⇒ ∠PTS = ∠PQR | Using (1)
⇒ ∠PTQ = ∠PQT ∴ PT = PQ
| Sides opposite to equal angles of a triangle are equal.
