Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

51. In the given figure, AE bisects ∠DAC and ∠B = ∠C, prove that AE || BC.

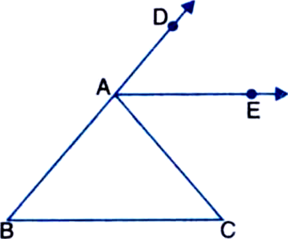
Given: AE bisects ∠DAC and ∠B = ∠C
To Prove: AE || BC
Proof: In ∆ABC,
Ext. ∠DAC = ∠ABC + ∠ACB ...(1)
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
⇒ ∠DAC = ∠ACB + ∠ACB
| ∵ ∠B = ∠C (Given)
⇒ ∠DAC = 2∠ACB
⇒ 2∠CAE = 2∠ACB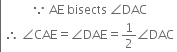

$left enclose table row cell because space AE space bisects space angle DAC end cell row cell therefore space angle CAE equals angle DAE equals 1 half angle DAC end cell end table end enclose$

⇒ ∠CAE = ∠ACB
But these angles form a pair of equal alternate interior angles
∴ AE || BC

1923 Views

52. If the bisector of the vertical angle of a triangle bisects the base of the triangle, then prove that the triangle is isosceles.

3437 Views

53. In figure, ∠BAC = 85°, ∠A - ∠B and BD = CD. Find the measure of ∠x, ∠y and ∠z. Give reasons to support your answer.

258 Views

54. In ∆ABC, the bisector AD of ∠A is perpendicular to side BC (see figure). Show that AB = AC and ∆ABC is isosceles.

410 Views

55. E and F are respectively the mid-points of equal sides AB and AC of ∆ABC (see figure). Show that BF = CE.

363 Views

56. In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD (see figure). Show that AD = AE.

801 Views

57. AD and BE are respectively the altitudes of an isosceles triangle ABC. in which AC = BC. Prove that AE = BD.

1518 Views

58. PS is an altitude of an isosceles triangle PQR in which PQ = PR. Show that PS bisects ∠P.

421 Views

59. In ∆ABC, AB = AC. D is a point in side ∆ABC such that BD = DC. Prove that ∠ABD = ∠ACD.

120 Views

60. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that AD is also the median of the triangle.

168 Views