 Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type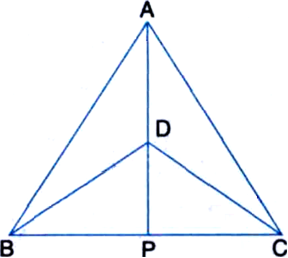
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Given: ∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. AD is extended to intersect BC at P.
To Prove: (i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Proof: (i) In ∆ABD and ∆ACD,
AB = AC ...(1)
| ∵ ∆ABC is an isosceles triangle
BD = CD ...(2)
| ∵ ADBC is an isosceles triangle
AD = AD ...(3) | Common
∴ ∆ABD ≅ ∆ACD | SSS Rule
(ii) In ∆ABP and ∆ACP,
AB = AC ...(4) | From(1)
∠ABP = ∠ACP ...(5)
| ∵ AB = AC From (1) ∴ ∠ABP = ∠ACP Angles opposite to equal sides of a triangle are
equal
∵ ∆ABD ≅ ∆ACD
| Proved in (i) above
∴ ∠BAP = ∠CAP ...(6) | C.P.C.T.
In view of (4), (5) and (6)
∆ABP ≅ ∆ACP | ASA Rule
(iii) ∵ ∆ABP ≅ ∆ACP
| Proved in (ii) above
∠BAP = ∠CAP | C.P.C.T.
⇒ AP bisects ∠A.
In ∆BDP and ∆CDP,
BD = CD ...(7) | From (2)
DP = DP ...(8) | Common
∵ ∆ABP ≅ ∆ACP
| Proved in (ii) above
∴ BP = CP ...(9) | C.P.C.T.
In view of (7), (8) and (9),
∆BDP ≅ ∆CDP | SSS Rule
∴ ∠BDP = ∠CDP | C.P.C.T.
⇒ DP bisects ∠D
⇒ AP bisects ∠D
(iv) ∵ ∆BDP ≅ ∆CDP
| Proved in (iii) above
∴ BP = CP ...(10) | C.P.C.T.
∠BPD = ∠CPD | C.P.C.T.
But ∠BPD + ∠CPD = 180°
| Linear Pair Axiom
∴ ∠BPD = ∠CPD = 90° ...(11)
In view of (10) and (11),
AP is the perpendicular bisector of BC.
 Short Answer Type
Short Answer TypeAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of triangle PQR (see figure). Show that:
(i) ∆ABM ≅ ∆PQN
(ii) ∆ABC ≅ ∆PQR.
The diagonals PR and QS of a quadrilateral PQRS intersect each other at O. Prove that
(i) PQ + QR + RS + SP > PR + QS
(ii) PQ + QR + RS + SP < 2 (PR + QS)
