Short Answer Type
Long Answer Type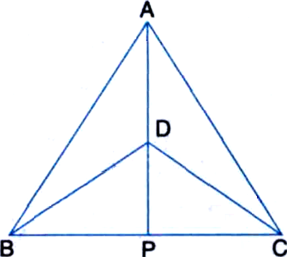
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Short Answer TypeAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A.
Given: AD is an altitude of an isosceles triangle ABC in which AB = AC.
To Prove: (i) AD bisects BC
(ii) AD bisects ∠A.
Proof: (i) In right ∆ADB and right ∆ADC,
Hyp. AB = Hyp. AC | Given
Side AD = Side AD | Common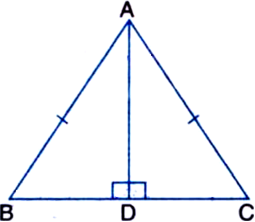
∴ ∆ADB ≅ ∆ADC | RHS Rule
∴ BD = CD | C.P.C.T.
⇒ AD bisects BC.
(ii) ∵ ∆ADB ≅ ∆ADC
| Proved in (i) above
∴ ∠BAD = ∠CAD | C.P.C.T.
⇒ AD bisects ∠A.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of triangle PQR (see figure). Show that:
(i) ∆ABM ≅ ∆PQN
(ii) ∆ABC ≅ ∆PQR.
The diagonals PR and QS of a quadrilateral PQRS intersect each other at O. Prove that
(i) PQ + QR + RS + SP > PR + QS
(ii) PQ + QR + RS + SP < 2 (PR + QS)
Switch
