Long Answer TypeLet 
be the position vectors of the vertices A, B, C, D of the trapezium in which AB||CD
Now AB || CD
where 
is some scalar.
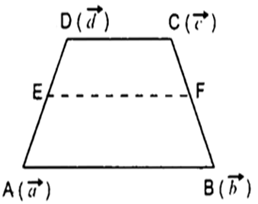
Let E be mid-point of AD and F be mid-point of BC.
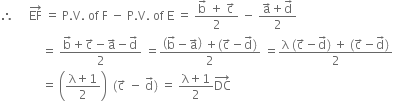
∴ EF and DC are parallel.
Also EF is parallel to AB as AB is parallel to DC.
Now, 
Hence the result.
, where O is any arbitrary point.
is parallel to 
where K divides AB in the ratio 1 : 3.
. The straight lines FD and AE intersect at the point O. Find the ratio 
and 
can form the sides of a triangle. Find the lengths of the medians of the triangle.
Short Answer Type
Switch
when
