 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type (i) Draw a circle with centre at O and radius = 1.
Let P, Q be two points on the circle such that
∠POX = α and ∠QQX = β.
∴ ∠POQ = α + β
Co-ordinates of P, Q are (cos α, sin α) and (cos β, – sin β) respectively.
(ii) Draw a circle with centre at O and radius = 1.
Let P, Q be two points on the circle such that
∠POX = α, ∠QOX = β
∴ ∠POQ = α – β
Co-ordinates of P, Q are (cos α, sin α) and (cos β, sin β) respectively.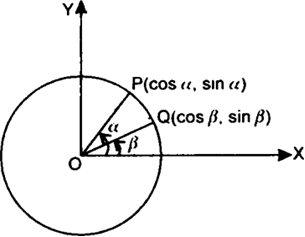
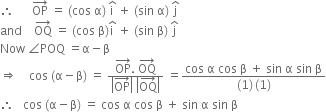
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type