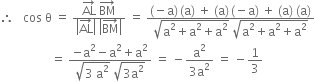230.
Show that the angle between two diagonals of a cube is 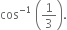
Take O, a comer of cube OBLCMANP, as origin and OA, OB, OC. the three edges through it as the axes.
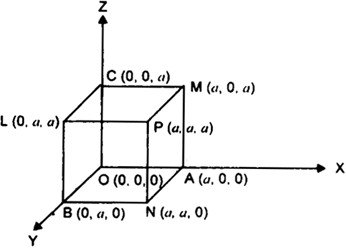
Let OA = OB = OC = α, then the co-ordinates of O, A, B, C are (0, 0, 0),
(a, 0. 0), (0, a, 0). (0, 0, a) respectively ; those of P, L, M, N are (a, a, a),(0, a. a), (a, 0, a), (a, a, 0) respectively.
The four diagonals are
OP, AL, BM, CN.
Consider the diagonals AL and BM

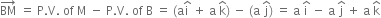
Let

be angle
between AL and BM.
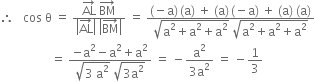



Similarly the angle between the other pairs of diagonals is
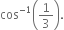
82 Views
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type