 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeIf ![]() are the position vectors of the non-collinear points A, B, C respectively in space, show that
are the position vectors of the non-collinear points A, B, C respectively in space, show that ![]() is perpendicular to plane ABC.
is perpendicular to plane ABC.
 Long Answer Type
Long Answer TypeLet ![]() be position vectors of A, B, C respectively.
be position vectors of A, B, C respectively.
From C, draw ![]() .
.![]()
In rt. ![]()
![]()
![]()
![]()
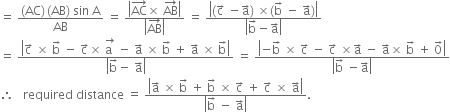
 Short Answer Type
Short Answer Type