 Short Answer Type
Short Answer TypeFind the coordinates of the point, where the line  intersects the plane
intersects the plane  . Also find the angle between the line and the plane.
. Also find the angle between the line and the plane.
Find the vector equation of the plane which contains the line of intersection of the planes.  and
and  and which is perpendicular to the plane
and which is perpendicular to the plane 
 Long Answer Type
Long Answer TypeFind the vector equation of the plane passing through three points with position vectors  Also, find the coordinates of the point of intersection of this plane and the line
Also, find the coordinates of the point of intersection of this plane and the line 
Let the position vectors of the three points be, 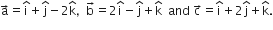
So, the equation of the plane passing through the point 
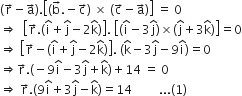
So, the vector equation of the required plane is 
The equation of the given line is 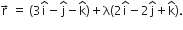
Position vector of any point on the given line is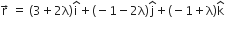 ....(2)
....(2)
The point (2) lies on plane (1) if, 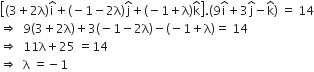
Putting  in (2), we have
in (2), we have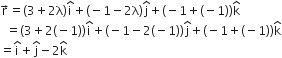
Thus, the position vector of the point of intersection of the given line and plane (1) is 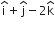 and its co-ordinates are (1, 1, -2).
and its co-ordinates are (1, 1, -2).
If  are mutually perpendicular vectors of equal magnitudes, show that the vector
are mutually perpendicular vectors of equal magnitudes, show that the vector  is equally
is equally  inclined to Also, find the angle which
inclined to Also, find the angle which  with
with  .
.

 coplanar.
coplanar. coplanar.
coplanar.
 Short Answer Type
Short Answer TypeFind the magnitude of each of the two vectors , having the same magnitude such that the angle between them is 60o and their scalar product is 9/2.
