A vertical pole of length a stands at the centre of a horizontal regular hexagonal ground of side a. A rope that is fixed taut in between a vertex on the ground and the tip of the pole has a length

• a

• $\sqrt{2\mathrm{a}}$

• $\sqrt{3\mathrm{a}}$

• $\sqrt{6\mathrm{a}}$

A peacock perched on the top of a 12 m high tree spots a snake moving towards its hole at the base of the tree from a distance equal to thrice the height of the tree. The peacock flies towards the snake in straight line and they both move at the same speed. At what distance from the base of the tree will the peacock catch the snake?

• 16 m

• 18 m

• 14 m

• 12m

63.

The cities of a country are connected by intercity roads. If a city is directly connected to an odd number of other cities, it is called an odd city. If a city is directly connected to an even number of other cities, it is called an even city. Then which of the following is impossible?

• There are an even number of odd cities.

• There are an odd number of odd cities.     

• There are an even number of even  cities.  

• There are an odd number of even cities. 

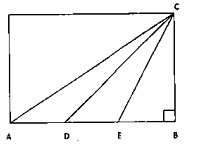
In the figure angle ABC = $\mathrm{\pi }$/2

AD = DE = EB

What is the ratio of the area of $∆$ADC to that of $∆$CDB?

• 1 : 1

• 1 : 2

• 1 : 3

• 1 : 4

A string of diameter 1mm is kept on a table in the shape of a close flat spiral, i.e. a spiral with no gap between the turns. The area of the table occupied by the spiral is 1 m². Then the length of the string is

• 10 m

• 10² m

• 10³ m

• 10⁶ m

25% of 25% of a quantity is x% of the quantity where x is

• 6.25%

• 12.5%

• 25%

• 50%

In the figure below, angle ABC = $\mathrm{\pi }$/2. I, II, III are the areas of semicircles on the sides opposite angles B, A and C respectively. Which of the following is always true?

• II² + III² = I²

• II + III = I    

• II² + III² > I²

• II + III < I

What is the minimum number of days between one Friday the 13^th and the next Friday the 13^th (Assume that the year is a leap year).

• 28

• 56

• 91

• 84

In a museum there were old coins with their respective years engraved on them, as follows:

(A) 1837 AD    (B) 1907 AD    (C) 1947 AD     (D) 200 BC

Identify the fake coin (s)

• Coin A

• Coin D

• Coin A and Coin B

• Coin C

Cucumber contains 99% water. Ramesh buys 100 kg of cucumbers. After 30 days of storing, the cucumbers lose some water. They now contain 98% water. What is the total weight of cucumbers now?

• 99 kg

• 50 kg

• 75 kg

• 2 kg