 Multiple Choice Questions
Multiple Choice QuestionsThe area bounded by the curves y = cos(x) and y = sin(x ) between the ordinates x = 0 and x = 3π/2
( 4√2 - 2 ) sq units
( 4√2 + 2 ) sq units
( 4√2 - 1 ) sq units
( 4√2 + 1 ) sq units
The area in the first quadrant between x2 + y2 = and y = sin(x) is
![]()
![]()
![]()
![]()
A.
![]()
x2 + y2 = π2 is a circle of radius m and centre at origin.
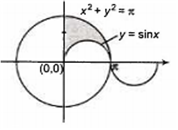
Required area

The area bounded by y = xelxl and lines lxl = 1, y = 0 is,
4 sq units
6 sq units
1 sq unit
2 sq unit
For which of the following values of m, the area of the region bounded by the curve y = x - x2 and the line y = mx equals 9/2
- 4
- 2
2
4
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4, the line x = √3y and x - axis is
π sq units
π/2 sq units
π/3 sq units
None of these
The area enclosed by y = 3x - 5, y = 0, x = 3 and x = 5 is
12 sq units
13 sq units
sq units
14 sq units
The area bounded by the curve y = | sin(x) |, x-axis and the lines | x | = π, is
2 sq unit
1 sq unit
4 sq unit
None of these
The line divides the area of the region bounded by y = sin(x), y = cos(x) and x - axis into two regions of areas A1 and A2. Then, A1 : A2 equals
4 : 1
3 : 1
2 : 1
1 : 1
The area of the region bounded by the straight lines x = 0 and x = 2x and the curves y = 2 and y = 2x - x2 is equal to
