21.

For the Hyperbola  which of the following remains constant when α varies?

• Eccentricity

• Directrix

• Abscissae of vertices

• Abscissae of vertices

The equation of a tangent to the parabola y² = 8x is y = x + 2. The point on this line from which the other tangent to the parabola is perpendicular to the given tangent is

• (−1, 1)

• (0, 2)

• (2, 4)

• (2, 4)

The locus of the vertices of the family of parabolas 

In an ellipse, the distance between its foci is 6 and minor axis is 8. Then its eccentricity is

• 3/5

• 1/5

• 2/5

• 2/5

If the lines 3x − 4y − 7 = 0 and 2x − 3y − 5 = 0 are two diameters of a circle of area 49π square units, the equation of the circle is

• x² + y² + 2x − 2y − 47 = 0

• x² + y² + 2x − 2y − 62 = 0

• x² + y² − 2x + 2y − 62 = 0

• x² + y² − 2x + 2y − 62 = 0

Let C be the circle with centre (0, 0) and radius 3 units. The equation of the locus of the mid points of the chords of the circle C that subtend an angle of 2π/3  at its centre is

• x²+y² = 3/2

• x² + y² = 1

• x²+y² = 27/4

• x²+y² = 27/4

Area of the greatest rectangle that can be inscribed in the ellipse 

• 2ab

• ab

• 
• 

Let P be the point (1, 0) and Q a point on the locus y² = 8x. The locus of mid point of PQ is

• y² – 4x + 2 = 0

• y² + 4x + 2 = 0

• x² + 4y + 2 =

• x² + 4y + 2 =

• an ellipse

• a circle

• a straight line

• a straight line

The locus of a point P (α, β) moving under the condition that the line y = αx + β is a tangent to the hyperbola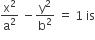 

• an ellipse

• a circle

• a parabola

• a parabola