 Multiple Choice Questions
Multiple Choice QuestionsIf the circles x2 + y2 + 2ax + cy + a = 0 and x2 + y2 – 3ax + dy – 1 = 0 intersect in two distinct points P and Q then the line 5x + by – a = 0 passes through P and Q for
exactly one value of a
no value of a
infinitely many values of a
infinitely many values of a
A circle touches the x-axis and also touches the circle with centre at (0, 3) and radius 2. The locus of the centre of the circle is
an ellipse
a circle
a hyperbola
a hyperbola
If a circle passes through the point (a, b) and cuts the circle x2 + y2 = p2 orthogonally, then the equation of the locus of its centre is
x2 + y2 – 3ax – 4by + (a2 + b2 – p2 ) = 0
2ax + 2by – (a2 – b2 + p2 ) = 0
x2 + y2 – 2ax – 3by + (a2 – b2 – p2 ) = 0
x2 + y2 – 2ax – 3by + (a2 – b2 – p2 ) = 0
An ellipse has OB as semi-minor axis, F and F′ its focii and the angle FBF′ is a right angle. Then the eccentricity of the ellipse is
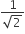
1/2
1/4
1/4
If the pair of lines ax2 + 2(a + b)xy + by2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then
3a2 – 10ab + 3b2 = 0
3a2 – 2ab + 3b2 = 0
3a2 + 10ab + 3b2 = 0
3a2 + 10ab + 3b2 = 0
If a circle passes through the point (a, b) and cuts the circle x2 +y2= 4 orthogonally, then the locus of its centre is
2ax +2by + (a2 +b2+4)=0
2ax +2by - (a2 +b2+4)=0
2ax -2by - (a2 +b2+4)=0
2ax -2by - (a2 +b2+4)=0
A variable circle passes through the fixed point A (p, q) and touches x-axis. The locus of the other end of the diameter through A is
(x-p)2 = 4qy
(x-q)2 = 4py
(y-p)2 = 4qx
(y-p)2 = 4qx
A.
(x-p)2 = 4qy
In a circle, AB is a diameter where the co-ordinate of A is (p, q) and let the co-ordinate of B is (x1 , y1 ).
Equation of circle in diameter form is (x - p)(x - x1 ) + (y - q)(y - y1 ) = 0
x2 - (p + x1 )x + px1 + y2 - (y1 + q)y + qy1 = 0
x2 - (p + x1 )x + y2 - (y1 + q)y + px1 + qy1 = 0
Since this circle touches X-axis
∴ y = 0
⇒ x2 - (p + x1 )x + px1 + qy1 = 0 Also the discriminant of above equation will be equal to zero because circle touches X-axis.
∴ (p + x1 )2 = 4(px1 + qy1) p2 + x21 + 2px1
= 4px1 + 4qy1 x21 - 2px1 + p2 = 4qy1
Therefore the locus of point B is, (x - p)2 = 4qy
If the lines 2x + 3y + 1 = 0 and 3x – y – 4 = 0 lie along diameters of a circle of circumference 10π, then the equation of the circle is
x2 + y2- 2x +2y -23 = 0
x2 - y2- 2x -2y -23 = 0
x2 - y2- 2x -2y +23 = 0
x2 - y2- 2x -2y +23 = 0
If a ≠ 0 and the line 2bx + 3cy + 4d = 0 passes through the points of intersection of the parabolas y2+ 4ax = and x2+ 4ay = , then
d2 + (2b+3c)2 = 0
d2 +(3d+2c2) = 0
d2 + (2b-3c)2 = 0
d2 + (2b-3c)2 = 0
