 Multiple Choice Questions
Multiple Choice QuestionsIf the vertex of the conic y - 4y = 4x - 4a always lies between the straight lines x + y = 3 and 2x + 2y - 1 = 0, then
2 < a < 4
0 < a < 2
B.
Equation of the vertex of conic,
y2 - 4y = 4x - 4a
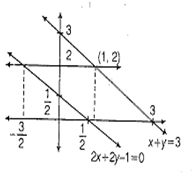
From figure,
Clearly,
The locus of the mid-points of chords of the circle x2 + y2 = 1, which subtends a right angle at the origin, is
x2 + y2 =
xy = 0
x2 - y2 = 0
The points of the ellipse 16x2 + 9y2 = 400 at which the ordinate decreases at the same rate at which the abscissa increases is/are given by
If the parabola x2 = ay makes an intercept of length units on the line y - 2x = 1, then a is equal to
1
- 2
- 1
2
If the vertex of the conic y - 4y = 4x - 4a always lies between the straight lines x + y = 3 and 2x + 2y - 1 = 0, then
2 < a < 4
0 < a < 2
If the point lies in the region between the lines x + y = 2 and x - y = 2 containing the origin, then 0 lies in
Let 16x2 - 3y - 32x - 12y = 44 represents a hyperbola. Then,
length of the transverse axis is
length of each latusrectum is
eccentricity is
equation of a directrix is x =
If the straight line (a - 1)x - by + 4 = 0 is normal to the hyperbola xy = 1, then which of the following does not hold?
a > 1, b > 0
a > 1, b < 0
a < 1, b < 0
a < 1, b > 0
