 Multiple Choice Questions
Multiple Choice QuestionsThe area of the region bounded by the parabola y = x2 - 4x + 5 and the straight line y= x + l is
2
3
If P be a point on the parabola y = 4ax with focus F. Let Q denote the foot of the perpendicular from P onto the directrix. Then, is
1
2
The equations of the circles, which touch both the axes and the line 4x + 3y = 12 and have centres in the first quadrant, are
x2 + y2 + x - y + 1 = 0
x2 + y2 - 2x - 2y + 1 = 0
x2 + y2 - 12x - 12y + 36 = 0
x2 + y2 - 6x - 6y + 36 = 0
If the circles x2 + y2 + 2x + 2ky + 6 = 0 and x2 + y2 + 2ky + k = 0 intersect orthogonally, then k is equal to
If four distinct points (2k, 3k), (2, 0), (0, 3), (0, 0) lie on a circle, then
k < 0
0 < k < 1
k = 1
k > 1
Let the foci of the ellipse subtend a right angle at a point P. Then, the locus of P is
x2 + y2 = 1
x2 + y2 = 2
x2 + y2 = 4
x2 + y2 = 8
Let P be the mid-point of a chord joining the vertex of the parabola y2 = 8x to another point on it. Then, the locus of P is
y2 = 2x
y2 = 4x
= 1
The line x = 2y intersects the ellipse at the points P and Q. The equation of the circle with PQ as diameter is
x2 + y2 = 1
x2 + y2 = 2
x2 + y2 =
D.
x2 + y2 =
Solving x = 2y ...(i)
and ...(ii)
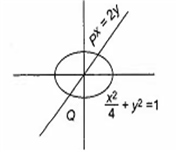
Put x = 2y in Eq. (ii), we get
The eccentric angle in the first quadrant of a point on the ellipse at a distance units from the centre of the ellipse is
