 Multiple Choice Questions
Multiple Choice QuestionsEquation of tangent to the circle x2 + y2 - 2x - 2y + 1 = 0 perpendicular to y = x is given by
None of these
The locus of centre of circles which cuts orthogonally the circle x2 + y2 - 4x + 8 = 0 and touches x + 1 = 0, is
y2 + 6x + 7 = 0
x2 + y2 + 2x + 3 = 0
x2 + 3y + 4 = 0
None of the above
The radical centre of the system of circles
x2 + y2 + 4x + 7 = 0,
2(x2 + y2) + 3x + 5y + 9 = 0
and x2 + y2 + y = 0 is
(- 2, - 1)
(1, - 2)
(- 1, - 2)
None of these
The point on the straight line y = 2x + 11 which is nearest to the circle 16(x2 + y) + 32x - 8y - 50 = 0, is
The locus of the extrimities of the latusrectum of the family of ellipses b2x2 + y2 = a2b2 having a given major axis, is
The number of common tangents to two circles x2 + y2 = 4 and x2 + y2 - 8x + 12 = 0 is
1
2
3
4
C.
3
The figure of both the circles are shown below
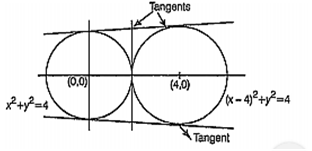
From figure, we see that there is exactly three common tangents.
If the tangent at the point of the hyperbola is parallel to 3x - y + 4 = 0, then the value of is
If an equilateral triangle is inscribed in the circle x2 + y2 = a2, the lenth of its each side is
If the vertex is (3,0) and the extremities of the latusrectum are (4, 3) and (4, - 3), then the equation of the parabola is
y2 = 4(x - 3)
x2 = 4(y - 3)
y2 = - 4(x + 3)
x2 = - 4(y + 3)
