 Multiple Choice Questions
Multiple Choice QuestionsEquation of tangent to the circle x2 + y2 - 2x - 2y + 1 = 0 perpendicular to y = x is given by
None of these
The locus of centre of circles which cuts orthogonally the circle x2 + y2 - 4x + 8 = 0 and touches x + 1 = 0, is
y2 + 6x + 7 = 0
x2 + y2 + 2x + 3 = 0
x2 + 3y + 4 = 0
None of the above
The radical centre of the system of circles
x2 + y2 + 4x + 7 = 0,
2(x2 + y2) + 3x + 5y + 9 = 0
and x2 + y2 + y = 0 is
(- 2, - 1)
(1, - 2)
(- 1, - 2)
None of these
The point on the straight line y = 2x + 11 which is nearest to the circle 16(x2 + y) + 32x - 8y - 50 = 0, is
The locus of the extrimities of the latusrectum of the family of ellipses b2x2 + y2 = a2b2 having a given major axis, is
If the tangent at the point of the hyperbola is parallel to 3x - y + 4 = 0, then the value of is
If an equilateral triangle is inscribed in the circle x2 + y2 = a2, the lenth of its each side is
If the vertex is (3,0) and the extremities of the latusrectum are (4, 3) and (4, - 3), then the equation of the parabola is
y2 = 4(x - 3)
x2 = 4(y - 3)
y2 = - 4(x + 3)
x2 = - 4(y + 3)
A.
y2 = 4(x - 3)
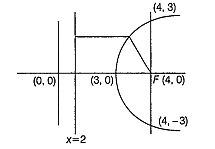
Equation of the parabola is
