 Multiple Choice Questions
Multiple Choice QuestionsIf P1, P2, P3 are the perimeters of the three circles
x2 + y2 + 8x - 6y = 0, 4x2 + 4y - 4x - 12y - 186 = 0 and x2 + y - 6x + 6y - 9 = 0 respectively, then
If the line 3x - 2y + 6 = 0 meets X-axis and Y-axis, respectively at A and B, then the equation of the circle with radius AB and centre at A is
x2 + y2 + 4x + 9 = 0
x2 + y2 + 4x - 9 = 0
x2 + y2 + 4x + 4 = 0
x2 + y2 + 4x - 4 = 0
A line l meets the circle x2 + y2 = 61 in A, B and P(- 5, 6) is such that PA = PB = 10. Then,the equation of l is
5x + 6y + 11 = 0
5x - 6y - 11 = 0
5x - 6y + 11 = 0
5x - 6y + 11 = 0
C.
5x - 6y + 11 = 0
Since, the line l meets the circle x2 + y2 = 61 at two points A and B.
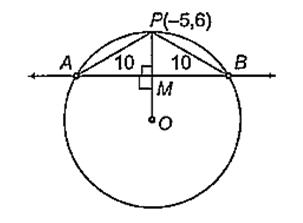
Thus, PM is perpendicular to AB and OM is perpendicular to the chord AB, therefore OP is perpendicular to AB.
If (1, a), (b, 2) are conjugate points with respect to the circle x2 + y2 = 25, then 4a + 2b is equal to
25
50
100
150
The equation of the circle whose diameter is the common chord of the circles x2 + y2 + 2x + 3y + 2 = 0 and x2 + y2 + 2x - 3y - 4 = 0 is
x2 + y2 + 2x + 2y + 2 = 0
x2 + y2 + 2x + 2y - 1 = 0
x2 + y2 + 2x + 2y + 1 = 0
x2 + y2 + 2x + 2y + 3 = 0
If x - y + 1 = 0 meets the circlex2 + y2 + y - 1 = 0 at A and B, then the equation of the circle with AB as diameter is
2(x2 + y2) + 3x - y + 1 = 0
2 (x2 + y2) + 3x - y + 2 = 0
2(x2 + y2) + 3x - y + 3 = 0
x2 + y2 + 3x - y + 1 = 0
