 Short Answer Type
Short Answer TypeFind the general solution of (x + log(y))dy + ydx = 0
Given equation can be rewritten as
(x + log(y))dy + ydx = 0
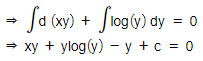
 Multiple Choice Questions
Multiple Choice QuestionsThe general solution of the differential equation
is
(A + B)e5x
(A + Bx)e- 4x
(A + Bx2)e4x
(A + Bx4)e4x
The general solution of the differential equation is
ex + e- y = C
ex + ey = C
ey + e- x = C
e- x + e- y = C
The differential equation of y = aebx (a and b are parameters) is
yy1 = y22
yy2 = y12
yy12 = y2
yy22 = y1
