 Multiple Choice Questions
Multiple Choice QuestionsMinimize : z = 3x + y, subject to 2x + 3y 6, x + y 1,
x = 1, y = 1
x = 0, y = 1
x = 1, y = 0
x = - 1, y = - 1
B.
x = 0, y = 1
Given, 2x + 3y = 6
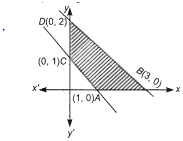
This line meets the axes at (3, 0) and (0, 2).
Now, x + y 1
This line meets the axes at (1, 0) and (0, 1).
Now, at A(1, 0), z = 3
at B (3, 0), z = 9 at C (0, 1), z = 1
at D (0, 2), z = 2
It is clear that minimum value of z = 3x + y is 1 at (0, 1).
Using Trapezoidal rule and following table is equal to
| x | 0 | 0 | 4 | 6 | 8 |
| f(x) | 2 | 5 | 10 | 17 | 26 |
184
92
46
- 36
