 Multiple Choice Questions
Multiple Choice QuestionsThe centroid of the triangle formed by the lines x + y = 1, 2x + 3y = 6 and 4x - y = - 4 lies in the quadrant
I
II
III
IV
For all values of a and b the line (a + 2b)x + (a - by + (a + 5b) = 0 passes through the point.
(- 1, 2)
(2, - 1)
(- 2, 1)
(1, - 2)
The orthocentre of triangle formed by the lines x + 3y = 10 and 6x2 + xy - y2 = 0 is
(1, 3)
(3, 1)
(- 1, 3)
(1, - 3)
A.
(1, 3)
The given lines are
x + 3y = 10 ...(i)
and 6x2 + xy - y2 = 0
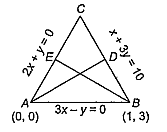
or 6x2 + 3xy - 2xy - y2 = 0
or 3x(2x + y) - y(2x + y) = 0
3x - y = 0 ...(ii)
2x + y = 0 ...(iii)
On solving Eqs. (i) and (ii), we get
A particle moves along the curve y = x2 + 2x. Then, the point on the curve such that x and y coordinates of the particle change with same rate is
(1, 3)
(- 1, - 1)
If PM is the perpendicular from P(2, 3) onto the line x + y = 3, then the coordinates of M are
(2, 1)
(- 1, 4)
(1, 2)
(4, - 1)
If OA is equally inclined to OX, OY and OZ and if A is units from the origin, then A is :
(3, 3, 3)
(- 1, 1, - 1)
(- 1, 1, 1)
(1, 1, 1)
